Voluntary participation in large-scale collaboration events tends to follow a power law: a few people contribute a lot, while many people contribute only a little. For background and examples see this poster summarizing power laws in online innovation forums and browse my innovation-related publications and presentations.
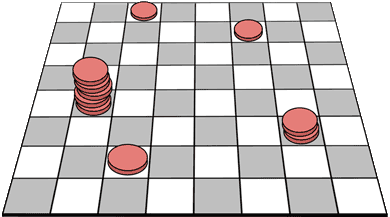
Below you'll find a simple model with only one variable parameter that does a remarkably good job reproducing observed participation statistics. The checkboard sketch helps explain how it works:
- The squares are our potential audience. Most of them are empty; they're "lurkers" who haven't participated yet.
- At each step of our simulation we add a new checker to the board according to "joining rules"...
- x% of the time we apply a "rich-get-richer" rule, otherwise a "random" rule. The percentage x is our only parameter; it's labelled "self-feedback" in the simulation below.
- The "rich-get-richer" rule says that we give the new checker to one of the squares that's already populated, proportionate to its current total. For example in the cartoon there are ten total checkers: one square has 5, one has 2, and the other three have 1 each. Therefore at this step there's a 5/10 chance the new piece will go to the biggest stack, a 2/10 chance it will go to the stack of 2, and a 3/10 chance it will go to one of the singleton squares.
- The "random" rule simply says that the new checker goes to any square, picked at random. For a large checkerboard this becomes equivalent to adding to an unoccupied square.
- See Bagrow et al. for a proof that this game generates a power law (in the limit of a large checkerboard), and Newman for a very good review of power laws in theory and experience. If you pursue this literature, note that our "self feedback" parameter is Bagrow's "r", and is related to the exponents of power laws (α, as Newman and most others describe them) as α = 1 + 1/r, or r = 1/(α-1).
Thinking About Slopes
Because power laws appear so often in real collaboration data, and because there's only one parameter which governs them, it's worth considering what affects the value of that parameter in real situations. This table lists a few examples and possible "explanations":| example | parameters | "explanations" | ||||
|---|---|---|---|---|---|---|
| alpha | self-feedback | for me — for us | persistent — transient | easy — hard | general — specific | |
| 2.04 | 96% | incentive to join << incentive to stay | always available | easy to contribute | general topics, lots to say | |
| "80-20 rule" | 2.16 | 86% | ||||
| Wikipedia edits | 2.28 | 78% | ||||
| business challenges | 2.7-3.0 | 60-50% | incentive to join >> incentive to stay | available for a limited time | hard to contribute | specific topics, limited individual knowledge |
Mathematical proof that a joining model (Bagrow, the checkers game above) and a quitting model (Wilkinson) will generate power laws doesn't tell us which (if either) is behind real data. Each of the explanatory factors in the table makes sense in various contexts; any or all (in combination) could lead to the behavior we see. Debating them isn't very fruitful; better to be scientific and consider experiments and data which might distinguish among them, and especially to consider which are within our control (like task complexity or duration) to bias our collaboration systems in desirable directions.
Funny thing about the slopes of power laws: they nearly always fall between α = 2 and α = 3 (which corresponds to self-feedback between 100% and 50%, respectively). The examples in this table show the full range of power law slope values seen, from Twitter (me, persistent, easy, general) to business challenges (us, transient, hard, specific). Systems with α > 3 aren't seen, perhaps because they're inherently fragile or they collapse to simple Gaussian "average participation". An informal explanation is that "unless there's enough in it for me," a feedback-driven system cannot be sustained. And now we know that "enough" means 50% to 100% of the goodies. Isn't it strange when an incredibly simple model (that matches huge observed datasets) suggests a quantitative limit to altruism ?
Also note that there's nothing here about networks. Whether you get a new checker in the model depends on your own inventory, otherwise new players enter at random, maybe next to you or maybe far across the board. Because networks beget power laws, the converse is often assumed true: that an observed power law in human behavior implies an underlying network as key to the positive feedback — but this model and Occam's Razor suggest that's not necessarily so.